티스토리 뷰
백준 1799, 비숍 문제설명
1799번: 비숍
첫째 줄에 체스판의 크기가 주어진다. 체스판의 크기는 10이하의 자연수이다. 둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로
www.acmicpc.net

비숍문제는 백트래킹 대표 문제 중 하나인 N-Queen의 상위호환 문제입니다.
단순 백트래킹 개념만 사용할게 아니라, 비숍이라는 체스말의 특성까지 잘 활용해야 시간초과없이 수행해야 통과할 수 있는 문제입니다.
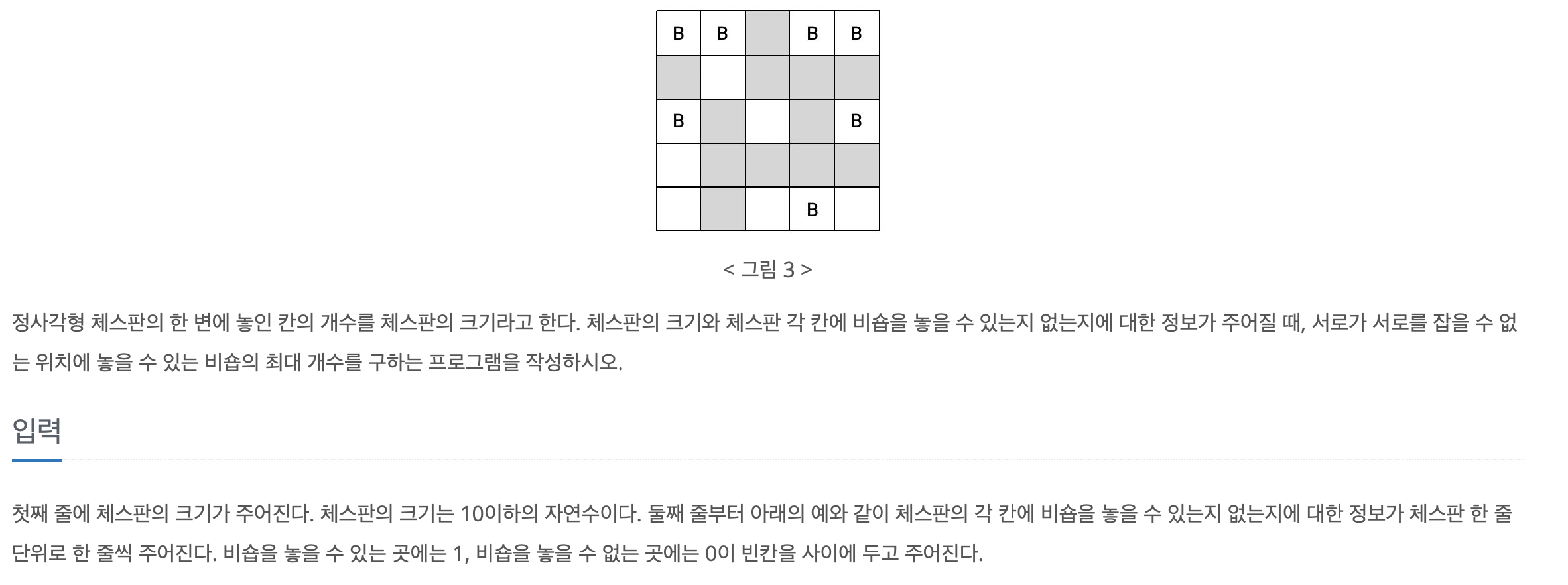
체스판의 크기와 비숍 말을 둘 수 있는 위치가 주어졌을때, 서로가 서로를 잡을 수 없게하는 조건을 충족하면서 가장 많은 비숍을 둘 수 있는 경우를 찾는 문제입니다.

체스판의 너비를 입력받은 후, N x N 크기의 체스판에 비숍 말을 둘 수 있는 지 여부를 1, 0으로 표현해서 입력받습니다. 여기에서 1로 되어있는 곳에 한해서 비숍 말을 배치할 수 있습니다.
만약 단순 백트래킹을 수행할 경우, 각각의 위치에 비숍을 두냐, 안두냐 두가지의 경우가 생기며, 이를 완전탐색으로 계산하면 O(2^(N*N))의 시간복잡도를 기대해볼 수 있습니다.
하지만 여기에서 비숍의 특성을 이용해보면, "하얀, 검은 칸에 있는 비숍은 동일한 색상의 칸만 이동할 수 있다." 를 통해서 체스판의 하얀칸에 대한 최대 비숍 배치가능 수 + 검은칸에 대한 최대 비숍 배치가능 수를 나눠서 구해도 문제가 없다는 것을 알 수 있습니다. 하얀칸의 비숍은 절대로 검은칸의 비숍을 잡을 수 없기 때문이죠.
체스판의 흑, 백 영역에 배치된 비숍끼리는 서로 공격이 불가능하다는 점을 참고해서 알고리즘을 작성하면, 시간복잡도를 O(2^(N*N)) -> O(2^(N/2*N/2))로 줄일 수 있습니다.
이 개념을 활용해서 바로, 스위프트 언어를 통해 비숍문제 풀어보도록 하겠습니다.
백준 1799, 비숍 백트래킹 backtracking swift 문제풀이

체스판 상태를 입력받을때 사용할 클로져입니다. 그냥 [Int]타입을 반환하는 함수로 구현해도 되지만, 저는 평소에 사용하지 않는 형태로 연습하는 것을 좋아해서 이렇게도 구현해서 사용하곤 합니다. 그냥 split이나 components를 사용해도 문제없을거에요.
swift Input Code

체스판 너비, N을 입력받습니다. 그리고 정답변수 ans, 최대 배치가능한 비숍 갯수 카운팅 용 변수 count를 선언합니다. 21행의 t 배열은 실제로 사용안하므로 무시부탁드려요.
22 ~24행) 체스판의 상태를 G에 입력받고 있습니다.
흰색칸, 검정색칸의 비숍 배치가능 위치정보를 저장한다.

26 ~ 27행) AV, BV는 각각 체스판의 검은색상, 흰색상의 배치가능한 위치정보를 담습니다.
29 ~ 40행) 그래프의 값이 1일 경우는 비숍이 배치가능한 경우죠. 이 경우에는 현재 위치가 검은영역인지, 흰영역인지에 따라서 AV, BV에 위치정보를 저장해줍니다. 여기에서 st라는 값을 추가로 보는 이유는, 체스판은 N번째 줄이 흰색칸으로 시작한다면, N+1번째 줄은 검은칸으로 시작하므로 이를 이용해서 현재 행이 짝수, 홀수 냐에 따라 구분지어서 체크하는데 사용합니다. (이해 안가신다면 디버깅해보세요.)
특정 위치의 비숍이 이전에 배치한 비숍을 잡아먹는지 체크하는 메서드 구현

43행) C는 AV, BV의 i번째 위치에 비숍이 배치되었는지를 true, false로 체크하는데에 사용합니다. 예를들어서 AV에대한 비숍 배치를 체크하는 경우, C[i] 가 true라면, AV[i] 위치의 비숍이 이미 배치되어있음을 의미합니다.
45행) 특정 위치의 비숍이 배치가능한지 체크합니다. inout으로 받는 V는 AV, BV가 call by reference 방식처럼 넘겨져서 사용됩니다.
46 ~ 48행) 현재 배치되는 위치 이전에 배치될 수 있는 모든 위치정보를 순회해봅니다. 이때 만약 이전에 배치되지 않은 위치정보일 경우에는 해당 위치에 비숍이 배치되지 않았으므로, 잡아먹히는지를 체크할 필요가 없습니다. 그러므로 이 경우에는 continue로 넘어가서 다음 위치정보를 체크합니다. (48행)
49 ~ 53행) 비숍은 대각선으로만 움직입니다. 즉, 새로 비숍을 배치할 위치와 이전에 배치한 비숍의 위치 간의 x, y 절대값 차이가 동일하게 되면, 대각선으로 잡아먹힐 수 있음을 의미합니다. 이때는 배치불가하므로 false를 반환해줍니다.(53행)
56행) 이렇게 이전에 배치되었던 모든 비숍에 대해서 잡아먹히는 상황이 아니면, 배치가능하므로, true를 반환합니다.
각각의 배치가능 위치에 비숍을 둘 수 있는지 체크, 백트래킹을 수행한다.

앞서 구현한 canPlace 메서드를 활용해서 백트래킹을 수행합니다. 서두에 말씀드렸듯이, 이 백트래킹은 검정칸의 최대 배치가능한 비숍의 수를 구하고, 백색칸의 최대 배치가능 비숍 수를 구하는 2번의 케이스에 대한 백트래킹을 수행하여 시간복잡도를 줄일 수 있습니다.
67 ~ 71행) 만약 해당 x, y위치에 비숍배치가 가능하면, 비숍을 배치하고, 재귀를 통해 다음 경우에 대한 탐색을 수행합니다. 만약 배치가 불가능하다면, 다음 위치에 비숍을 둘 수 있는지 보지요.
백색, 검정색 칸 2가지 케이스에 대한 최대 비숍배치가능 수를 카운팅 한다.
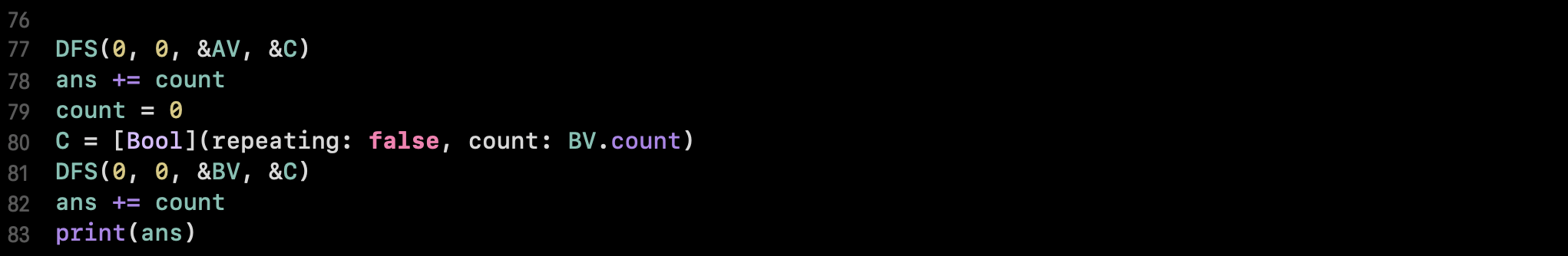
앞서 말했던ㄴ 2번의 케이스에 대한 백트래킹을 수행하는 메인함수 코드입니다. 백색(예) 칸에 대한 배치가능 정보가 있는 AV, 검정색(예) 칸에 대한 배치가능 정보가 있는 BV 위치정보를 참고하여 백트래킹을 수행합니다.
77 ~ 78행) AV 위치정보에 대한 백트래킹을 수행해서 최대 배치가능한 비숍 수를 count에 카운팅, ans에 누적시킵니다.
79 ~ 83행) count 변수를 0으로 초기화 하고, 이번에는 BV 위치정보에 대한 비숍 수를 카운팅 하여 ans에 누적시킵니다. 이후 백색칸의 최대 배치가능 수 + 검정색칸의 최대 배치가능 수가 저장된 ans변수를 결과로 출력합니다.
제출결과 및 전체 소스코드는 아래와 같습니다. 풀었던 직후의 작성코드를 그대로 사용한 터라 일부 코드가 지저분한것 같은데요. 관련 질문 및 의견 언제든 환영합니다. 즐거운 하루 되세요!
백준 1799, 비숍 swift 풀이결과 및 전체 소스코드

let ip: (() -> [Int]) = {
var result: [Int] = []
readLine()!.forEach { char in
if char == " " { return }
result.append(char == "1" ? 1 : 0)
}
return result
}
let N = Int(readLine()!)!
var ans = 0, count = 0
var G = [[Int]]()
var t = [Int]()
(0..<N).forEach { _ in
G.append(ip())
}
var AV = [(Int, Int)]()
var BV = [(Int, Int)]()
for i in G.indices {
let flag = i % 2 == 0
let st = flag ? 0 : 1
for j in G[i].indices {
if G[i][j] == 1 {
if (st+j) % 2 == 0 {
AV.append((i, j))
} else {
BV.append((i, j))
}
}
}
}
var C = [Bool](repeating: false, count: AV.count)
func canPlace(at x: Int, y: Int, to: Int, _ V: inout [(Int, Int)], _ C: inout [Bool]) -> Bool {
for i in 0...to {
let p = (x: V[i].0, y: V[i].1)
if (p.x == x && p.y == y) || !C[i] { continue }
var dx = p.x - x
dx *= dx > 0 ? 1 : -1
var dy = p.y - y
dy *= dy > 0 ? 1 : -1
if dx == dy { return false }
}
return true
}
func DFS(_ bdx: Int, _ cnt: Int, _ V: inout [(Int, Int)], _ C: inout [Bool]) {
if bdx >= V.count { return }
let originC = C
for i in V[bdx...].indices {
let pos = V[i]
let x = pos.0
let y = pos.1
if canPlace(at: x, y: y, to: i, &V, &C) {
C[i] = true
count = count < cnt+1 ? cnt+1 : count
DFS(i+1, cnt+1, &V, &C)
}
C = originC
}
}
DFS(0, 0, &AV, &C)
ans += count
count = 0
C = [Bool](repeating: false, count: BV.count)
DFS(0, 0, &BV, &C)
ans += count
print(ans)
'알고리즘 정보 > Swift 알고리즘' 카테고리의 다른 글
| 백준 13565 침투, DFS 깊이우선탐색 swift언어 문제풀이 (0) | 2022.02.07 |
|---|---|
| 백준 2331, 반복수열 swift dictionary, 거듭제곱 풀이 (0) | 2021.12.25 |
| 종만북 비트마스크 연산자 기본예제, swift언어로 보기 (0) | 2021.11.21 |
| 백준 16956 늑대와 양, 실버문제 애드혹 알고리즘 swift 풀이 (0) | 2021.10.10 |
| 백준 17471, 게리맨더링 조합, 완전탐색 swift 문제풀이 (0) | 2021.10.02 |
- Total
- Today
- Yesterday
- 개발자문서
- swift string
- Protocol
- 자연어처리
- 백준swift
- swift concurrency
- swift언어
- 컬렉션
- 김프매매
- ios
- uikit
- swift reduce
- 알고리즘
- 백준알고리즘
- swift
- swift문제
- Collection
- CoreML
- Swift 알고리즘
- createML
- 프로그래머스swift
- 프로토콜
- 알고리즘문제
- 프로그래머스
- swift 문자열
- 스위프트
- swift알고리즘
- swift 기초
- 부스트코스
- SwiftUI
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
