티스토리 뷰
안녕하세요~ 🤗
오늘은 백준 알고리즘문제, 용액 2467을 swift 언어를 활용해 풀어보도록 하겠습니다.
2467번: 용액
첫째 줄에는 전체 용액의 수 N이 입력된다. N은 2 이상 100,000 이하의 정수이다. 둘째 줄에는 용액의 특성값을 나타내는 N개의 정수가 빈칸을 사이에 두고 오름차순으로 입력되며, 이 수들은 모두 -
www.acmicpc.net
백준 용액 2467 문제 설명

백준 2467번 문제, 용액은 골드5에 랭크되어 있습니다.
스페셜 저지로 동일 입력값에 대해서 다수의 정답이 존재할 수 있는 문제입니다. 시간제한은 1초로, 1억번을 초과하는 연산이 있을 수 있는 경우를 주의해서 풀어야 할 것 같습니다.

해당 문제는 오름차순으로 정렬 된 용액 특성 값이 주어졌을때 두 개의 서로 다른 숫자를 섞어 0에 가장 가까운 용액을 만들어 내는 경우의 두 용액을 찾는 문제입니다.
가장 단순한 방법은 2중 포문을 통해서 서로 다른 값의 합을 계산한 후 그 합이 가장 최소의 절댓값을 가진 경우를 반환하면 끝나겠죠? 하지만, 그렇게 푼다면 입력값의 범위가 살짝만 커져도 시간초과(TLE)가 발생할 수 있습니다.
용액 입출력 예시
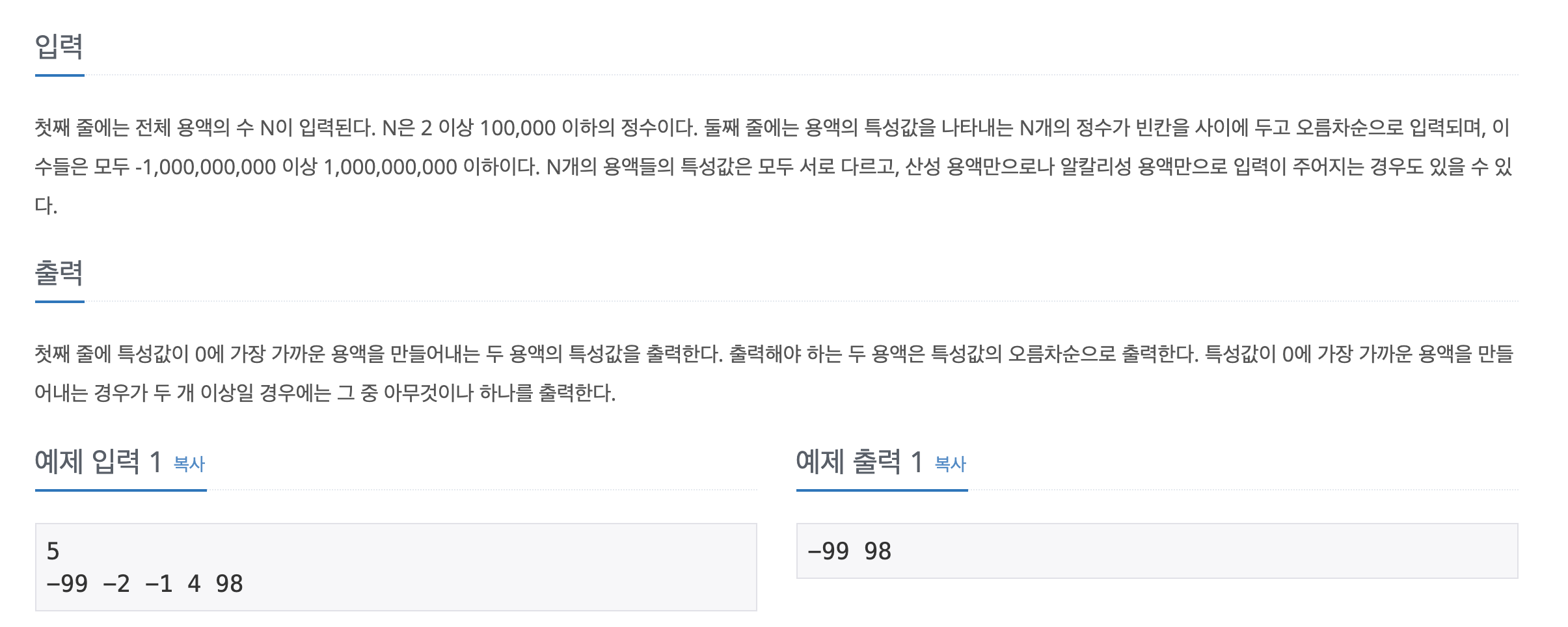
주어지는 값들은 -1e9 ~ 1e9의 범위를 갖고 있습니다. 단 두개의 합을 계산하는 것이기 때문에 cpp 등에서 int로 계산해도 문제는 없을 것 같고, Int의 기본 범위가 큰 swift에서는 당연히 문제가 없겠습니다.
중요하게 봐야 할 부분은 용액의 수 N의 범위가 2 이상 100,000이하의 범위라는 점입니다.
10만의 범위는 O(N^2)의 시간복잡도로 연산했을때 1억번의 연산을 훌쩍 넘습니다. 앞서 보았듯이 해당 문제의 시간제한은 1초입니다. 그러므로 O(N^2)의 시간복잡도로는 시간초과를 면치 못할 것입니다.
해당 문제는 이진탐색을 활용하면 O(NlogN)의 시간복잡도로 시간 내에 해결할 수 있습니다. 해당 시간복잡도면 충분히 100,000개의 용액 입력값이 들어와도 1초 이내에 해결할 수 있습니다.
용액 이진탐색 활용, swift 문제 풀이
let N = Int(readLine()!)!
let G = readLine()!.split(separator: " ").map { Int($0)! }
var MN = Int.max
var Ans = (0, 0)
먼저, 입력을 받겠습니다. 해당문제는 먼저 용액의 갯수를 입력으로 받습니다.
- N : 용액의 갯수를 받겠습니다. readLine() 함수는 문자열을 입력 받아 String? 타입을 받습니다. 해당 값을 강제 언래핑으로 받고, 또 다시 Int 형 변환을 위해 한번더 강제 언래핑 해줍니다.
- G : 용액의 값들을 한줄로 받습니다. 공백 단위로 값이 주어지기 때문에 split 메서드의 separator: 인자값을 활용해서 공백 단위로 쪼갠 뒤, map으로 쪼갠 값들을 Int형으로 강제언래핑 시도합니다.
- MN : 두 용액 합의 최소 절댓값을 비교하는데 사용합니다. 초기 값은 Int 형의 최댓값으로 셋팅합니다.
- Ans : 최소 절댓값이 발견되었을때 해당 용액의 값을 저장하여 이후 결과를 출력할때 사용합니다.
// MARK: G 배열을 순회하면서 이진탐색을 진행합니다.
// 이진탐색, logN을 N번 반복하므로 해당 알고리즘의 최종 시간 복잡도는 O(NlogN) 입니다.
for i in G.indices {
// G[i] 용액과 이 외의 용액의 합의 최소 절댓값을 이진탐색으로 연산
var left = i + 1
var right = N-1
// 이진탐색 진행
while left <= right {
let mid = (left + right) / 2
let sum = G[i] + G[mid]
var compSum = sum
// 절댓값은 음수가 나올 수 없으므로, 음수일 경우 -1을 곱해 절댓값을 구한다.
compSum *= sum < 0 ? -1 : 1
// 더 작은 절댓값이 나오면 갱신하고 그때의 두 용액의 값도 저장
if MN > compSum {
MN = compSum
Ans = (G[i], G[mid])
}
// 최소 절댓값이 0이 나오면 그 이상의 적은 절댓값은 없으므로 연산을 그대로 종료
if MN == 0 { break }
// 두 용액의 합이 0 미만이면 left값을 올려 합의 크기를 증가, 그 반대는 right값을 내려 합의 크기를 감소
// -> 정렬이 되어있기 때문에 가능한 이진탐색 간 비교
if sum < 0 {
left = mid + 1
} else {
right = mid - 1
}
}
if MN == 0 { break }
}
가장 핵심이 되는 용액 문제의 이진탐색 구현 부분입니다. 앞서 받았던 용액의 값들을 G.indices로 G의 계수범위 내 순회하며 이진탐색을 진행합니다.
이진탐색(logN)을 N번 진행해서 결과적으로 시간복잡도는 O(NlogN)입니다.
두 용액을 비교하는데 있어서 i번째 순회 간 첫번째 기준 용액은 G[i]로 고정됩니다. G[i] 용액과 비교할 용액은 i+1...G.count-1 범위의 용액이며 해당 범위의 용액들은 오름차순으로 정렬되어있으므로, 이진탐색의 조건을 충족하며 이진탐색을 활용해서 절댓값 합의 최소를 구할 수 있습니다.
이진탐색은 탐색할 범위의 수가 정렬되어있는 상태일 경우에 사용할 수 있으며, 탐색 간 시간복잡도는 O(logN) 입니다.
만약 두 용액의 최솟값이 0인 경우가 나온다면 이는 곧, 현재 두 개의 용액이 답이 될 수 있음을 의미합니다. 0 보다 적은 절댓값은 존재하지 않기 때문이죠.
만약 서로 합했던 두 용액의 합이 음수라면, 이진탐색 간의 좌측 포인터, left를 mid + 1로 올려 두 용액의 합을 키웁니다.
그 반대의 경우 right 포인터를 mid - 1로 내려서 두 용액의 합을 줄입니다. 이렇게 바뀔때마다 mid값은 변화된 (left + right) / 2의 값으로 갱신되어 비교하게 됩니다.
이렇게 logN번 탐색을 하면 결과적으로 G[i]와 i+1...G.count-1 범위의 두개의 용액을 합했을 때의 최소 절댓값을 알아 낼 수 있습니다.
그리고 결과적으로 이를 G 배열의 수 만큼 반복하여 연산하고 최소 절댓값과 그때의 두 용액의 값을 알 수 있게 됩니다.
// 최종적으로 정답을 출력
print(Ans.0, Ans.1, separator: " ")
// print("\(Ans.0) \(Ans.1)")
최종적으로 구한 두 용액의 값을 출력합니다. 두 개의 용액 값을 출력하는 방법은 위와 같이 다양한 방법 중 취향대로 작성하시면 됩니다.
오늘은 백준 골드5 알고리즘 중 하나인 용액문제를 이진탐색을 통해 풀어봤습니다.
이 문제는 앞서 소개한 방법대로 이진탐색을 활용해 O(NlogN)으로 풀 수 있는 문제이지만, 더욱 효율적인 O(N) 방법으로도 풀 수 있는 방법이 존재합니다.
해당 방법은 이진탐색으로 먼저 풀어보신 뒤 이후 어떻게 더 효율적으로 풀 수 있을 지 고민해보시면 좋을 것 같습니다. 🤗
'알고리즘 정보 > Swift 알고리즘' 카테고리의 다른 글
| Swift 알고리즘, 백준 1662 압축 스택 문제풀이 (0) | 2020.06.21 |
|---|---|
| Swift 알고리즘, 공백 유무 별 readLine 입력값 처리방법 (1) | 2020.06.04 |
| 프로그래머스 가장 먼 노드, 그래프 BFS swift 문제풀이 (0) | 2020.05.24 |
| 백준 1963 소수경로, BFS swift 알고리즘 문제 풀이 (0) | 2020.05.23 |
| 백준 3518 공백왕 빈-칸, 문자열 swift 알고리즘 문제 풀이 (0) | 2020.05.23 |
- Total
- Today
- Yesterday
- swift 기초
- Collection
- 프로그래머스swift
- Swift 알고리즘
- 부스트코스
- 프로토콜
- CoreML
- swift알고리즘
- swift문제
- swift string
- swift reduce
- createML
- swift 문자열
- Protocol
- 알고리즘문제
- uikit
- 백준알고리즘
- ios
- swift언어
- swift
- 개발자문서
- swift concurrency
- 백준swift
- SwiftUI
- 스위프트
- 컬렉션
- 알고리즘
- 자연어처리
- 김프매매
- 프로그래머스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
